Note

Go to the end to download the full example code.

biogeme.models¶

Examples of use of several functions.

This is designed for programmers who need examples of use of the functions of the module. The examples are designed to illustrate the syntax. They do not correspond to any meaningful model.

Michel Bierlaire Sun Jun 29 2025, 11:21:51

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from IPython.core.display_functions import display

from biogeme.calculator import evaluate_simple_expression_per_row
from biogeme.database import Database
from biogeme.expressions import Beta, Variable
from biogeme.models import (
    boxcox,
    cnl,
    cnlmu,
    get_mev_for_cross_nested,
    get_mev_for_cross_nested_mu,
    get_mev_for_nested,
    get_mev_for_nested_mu,
    logit,
    loglogit,
    logmev_endogenous_sampling,
    lognested,
    lognested_mev_mu,
    mev_endogenous_sampling,
    nested,
    nested_mev_mu,
    piecewise_formula,
    piecewise_function,
    piecewise_variables,
)
from biogeme.nests import (
    NestsForCrossNestedLogit,
    NestsForNestedLogit,
    OneNestForCrossNestedLogit,
    OneNestForNestedLogit,
)
from biogeme.second_derivatives import SecondDerivativesMode
from biogeme.version import get_text

Version of Biogeme.

print(get_text())

biogeme 3.3.1 [2025-09-03]
Home page: http://biogeme.epfl.ch
Submit questions to https://groups.google.com/d/forum/biogeme
Michel Bierlaire, Transport and Mobility Laboratory, Ecole Polytechnique Fédérale de Lausanne (EPFL)

Definition of a database¶

df = pd.DataFrame(
    {
        'Person': [1, 1, 1, 2, 2],
        'Exclude': [0, 0, 1, 0, 1],
        'Variable1': [1, 2, 3, 4, 5],
        'Variable2': [10, 20, 30, 40, 50],
        'Choice': [2, 2, 3, 1, 2],
        'Av1': [0, 1, 1, 1, 1],
        'Av2': [1, 1, 0, 1, 1],
        'Av3': [0, 1, 1, 1, 0],
    }
)
display(df)

   Person  Exclude  Variable1  Variable2  Choice  Av1  Av2  Av3
0       1        0          1         10       2    0    1    0
1       1        0          2         20       2    1    1    1
2       1        1          3         30       3    1    0    1
3       2        0          4         40       1    1    1    1
4       2        1          5         50       2    1    1    0

my_data = Database('test', df)

Piecewise linear specification¶

A piecewise linear specification (sometimes called ‘spline’) is a continuous but not differentiable function of the variable. It is defined based on thresholds. Between two thresholds, the function is linear. And the slope is changing after each threshold.

Consider a variable \(t\) and an interval \([a, a+b]\). We define a new variable

\[\begin{split}x_{[a,b]}(t) = \max(0,\min(t-a,b)) = \left\{ \begin{array}{ll} 0 & \text{if } t < a, \\ t-a & \text{if } a \leq t < a+b, \\ b & \text{otherwise}. \end{array} \right.\end{split}\]

For each interval \(]-\infty,a]\), we have

\[\begin{split}x_{]-\infty,a]}(t) = \min(t,a) = \left\{ \begin{array}{ll} t & \text{if } t < a, \\ a & \text{otherwise}. \end{array} \right..\end{split}\]

For each interval \([a,+\infty[\), we have

\[\begin{split}x_{]-\infty,a]}(t) = \max(0,t-a) = \left\{ \begin{array}{ll} 0& \text{if } t < a, \\ t-a & \text{otherwise}. \end{array} \right..\end{split}\]

If we consider a series of threshold

\[\alpha_1 < \alpha_2 < \ldots <\alpha_K,\]

the piecewise linear transform of variable \(t\) is

\[\sum_{k=1}^{K-1} \beta_k x_{[\alpha_k,\alpha_{k+1}]},\]

where \(\beta_k\) is the slope of the linear function in interval \([\alpha_k,\alpha_{k+1}]\).

The next statement generates the variables, given the thresholds. A None is equivalent to \(\infty\), and can only appear first (and it means \(-\infty\)) or last (and it means \(+\infty\)).

x = Variable('x')
thresholds = [None, 90, 180, 270, None]
variables = piecewise_variables(x, thresholds)
print(variables)

[BinaryMin(<Variable name=x>, <Numeric value=90.0>), BinaryMax(<Numeric value=0.0>, BinaryMin((<Variable name=x> - <Numeric value=90.0>), <Numeric value=90.0>)), BinaryMax(<Numeric value=0.0>, BinaryMin((<Variable name=x> - <Numeric value=180.0>), <Numeric value=90.0>)), BinaryMax(<Numeric value=0.0>, (<Variable name=x> - <Numeric value=270.0>))]

The next statement automatically generates the formula, including the Beta parameters, that are initialized to zero.

formula = piecewise_formula('x', thresholds)
print(formula)

MultipleSum((Beta('beta_x_minus_inf_90', 0, None, None, 0) * BinaryMin(x, `90.0`)), (Beta('beta_x_90_180', 0, None, None, 0) * BinaryMax(`0.0`, BinaryMin((x - `90.0`), `90.0`))), (Beta('beta_x_180_270', 0, None, None, 0) * BinaryMax(`0.0`, BinaryMin((x - `180.0`), `90.0`))), (Beta('beta_x_270_inf', 0, None, None, 0) * BinaryMax(`0.0`, (x - `270.0`))))

It is also possible to initialize the Beta parameters with other values. Note also that the first argument can be either the name of the variable (as in the previous call) or the variable itself.

betas = [-0.016806308, -0.010491137, -0.002012234, -0.020051303]
formula = piecewise_formula(x, thresholds, betas)
print(formula)

MultipleSum((`-0.016806308` * BinaryMin(x, `90.0`)), (`-0.010491137` * BinaryMax(`0.0`, BinaryMin((x - `90.0`), `90.0`))), (`-0.002012234` * BinaryMax(`0.0`, BinaryMin((x - `180.0`), `90.0`))), (`-0.020051303` * BinaryMax(`0.0`, (x - `270.0`))))

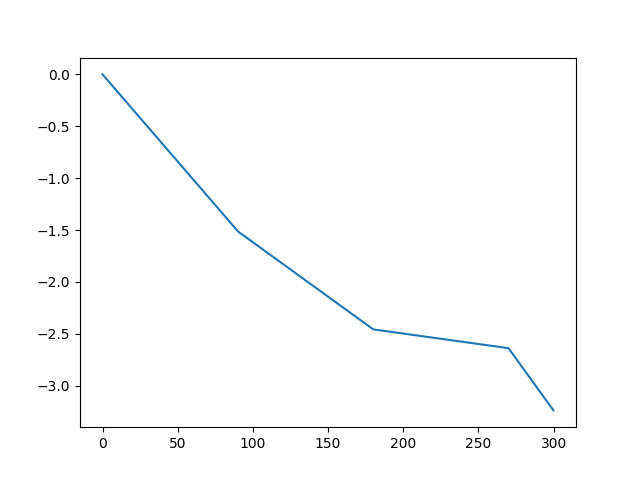
We provide a plot of a piecewise linear specification.

X = np.arange(0, 300, 0.1)
Y = [
    piecewise_function(
        x, thresholds, [-0.016806308, -0.010491137, -0.002012234, -0.020051303]
    )
    for x in X
]
plt.plot(X, Y)
plot models
[<matplotlib.lines.Line2D object at 0x477fb3750>]

Logit¶

v = {1: Variable('Variable1'), 2: 0.1, 3: -0.1}
av = {1: Variable('Av1'), 2: Variable('Av2'), 3: Variable('Av3')}

Calculation of the (log of the) logit for the three alternatives, based on their availability.

Alternative 1

p1 = logit(v, av, 1)
prob_1_value = evaluate_simple_expression_per_row(
    expression=p1,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Probability of alternative 1: {prob_1_value}')

Probability of alternative 1: [0.         0.78614804 0.95689275 0.9644926  0.99260846]

Alternative 2

p2 = logit(v, av, 2)
prob_2_value = evaluate_simple_expression_per_row(
    expression=p2,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Probability of alternative 2: {prob_2_value}')

Probability of alternative 2: [1.         0.11758308 0.         0.01952317 0.00739154]

Alternative 3

p3 = logit(v, av, 3)
prob_3_value = evaluate_simple_expression_per_row(
    expression=p3,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Probability of alternative 3: {prob_3_value}')

Probability of alternative 3: [0.         0.09626888 0.04310725 0.01598422 0.        ]

Calculation of the log of the logit for the three alternatives. If av is set to None, it means that all alternatives are always available. %% Alternative 1

p1 = loglogit(util=v, av=None, i=1)
log_prob_1_value = evaluate_simple_expression_per_row(
    expression=p1,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Log probability of alternative 1: {log_prob_1_value}')

Log probability of alternative 1: [-0.55356365 -0.24061016 -0.09537602 -0.03615312 -0.01345244]

Alternative 2

p2 = loglogit(util=v, av=None, i=2)
log_prob_2_value = evaluate_simple_expression_per_row(
    expression=p2,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Log probability of alternative 2: {log_prob_2_value}')

Log probability of alternative 2: [-1.45356365 -2.14061016 -2.99537602 -3.93615312 -4.91345244]

Alternative 3

p3 = loglogit(util=v, av=None, i=3)
log_prob_3_value = evaluate_simple_expression_per_row(
    expression=p3,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Log probability of alternative 3: {log_prob_3_value}')

Log probability of alternative 3: [-1.65356365 -2.34061016 -3.19537602 -4.13615312 -5.11345244]

Box-Cox transform¶

The Box-Cox transform of a variable \(x\) is defined as

\[B(x,\ell) =\frac{x^{\ell}-1}{\ell},\]

where \(\ell\) is a parameter that can be estimated from data. It has the property that

\[\lim_{\ell \to 0} B(x,\ell)=\log(x).\]
x = Variable('Variable1')
display(boxcox(x, 4))

{{0:{{0:((Variable1**4.0 - `1.0`) / `4.0`), 1:(((log(Variable1) + (`4.0` * log(Variable1)**2.0)) + ((`16.0` * log(Variable1)**3.0) / `6.0`)) + ((`64.0` * log(Variable1)**4.0) / `24.0`))}[((`1e-05` > `4.0`) * ((-`1e-05`) < `4.0`))], 1:`0.0`}[(Variable1 == `0.0`)]

x = Variable('Variable1')
display(boxcox(x, 0))

{{0:{{0:((Variable1**0.0 - `1.0`) / `0.0`), 1:(((log(Variable1) + (`0.0` * log(Variable1)**2.0)) + ((`0.0` * log(Variable1)**3.0) / `6.0`)) + ((`0.0` * log(Variable1)**4.0) / `24.0`))}[((`1e-05` > `0.0`) * ((-`1e-05`) < `0.0`))], 1:`0.0`}[(Variable1 == `0.0`)]

ell = Variable('Variable2')
e = boxcox(x, ell)
display(e)

{{0:{{0:(((Variable1 ** Variable2) - `1.0`) / Variable2), 1:(((log(Variable1) + (Variable2 * log(Variable1)**2.0)) + ((Variable2**2.0 * log(Variable1)**3.0) / `6.0`)) + ((Variable2**3.0 * log(Variable1)**4.0) / `24.0`))}[((Variable2 < `1e-05`) * (Variable2 > (-`1e-05`)))], 1:`0.0`}[(Variable1 == `0.0`)]

boxcox_value = evaluate_simple_expression_per_row(
    expression=e,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Box-Cox transform of Variable2: {boxcox_value}')

Box-Cox transform of Variable2: [0.00000000e+00 5.24287500e+04 6.86303774e+12 3.02231455e+22
 1.77635684e+33]

We numerically illustrate that, when \(\lambda\) goes to 0, the BoxCox transform of \(x\) converges to the log of \(x\).

for ell in range(1, 16):
    x = 3
    bc = boxcox(x, 10**-ell).get_value()
    print(f'ell=l0^(-{ell}): {bc:.6g} - {np.log(x):.6g} = {bc - np.log(x):.6g}')

ell=l0^(-1): 1.16123 - 1.09861 = 0.0626195
ell=l0^(-2): 1.10467 - 1.09861 = 0.00605691
ell=l0^(-3): 1.09922 - 1.09861 = 0.000603696
ell=l0^(-4): 1.09867 - 1.09861 = 6.03497e-05
ell=l0^(-5): 1.09862 - 1.09861 = 6.03476e-06
ell=l0^(-6): 1.09861 - 1.09861 = 1.20695e-06
ell=l0^(-7): 1.09861 - 1.09861 = 1.20695e-07
ell=l0^(-8): 1.09861 - 1.09861 = 1.20695e-08
ell=l0^(-9): 1.09861 - 1.09861 = 1.20695e-09
ell=l0^(-10): 1.09861 - 1.09861 = 1.20695e-10
ell=l0^(-11): 1.09861 - 1.09861 = 1.20695e-11
ell=l0^(-12): 1.09861 - 1.09861 = 1.20703e-12
ell=l0^(-13): 1.09861 - 1.09861 = 1.20792e-13
ell=l0^(-14): 1.09861 - 1.09861 = 1.19904e-14
ell=l0^(-15): 1.09861 - 1.09861 = 1.11022e-15

MEV models¶

MEV models are defined as

\[\frac{e^{V_i + \ln G_i(e^{V_1},\ldots,e^{V_J})}}{\sum_j e^{V_j + \ln G_j(e^{V_1},\ldots,e^{V_J})}},\]

where \(G\) is a generating function, and

\[G_i=\frac{\partial G}{\partial y_i}(e^{V_1},\ldots,e^{V_J}).\]

Nested logit model: the \(G\) function for the nested logit model is defined such that

\[G_i=\frac{\partial G}{\partial y_i}(e^{V_1},\ldots,e^{V_J}) = \mu e^{(\mu_m-1)V_i} \left(\sum_{i=1}^{J_m} e^{\mu_m V_i}\right)^{\frac{\mu}{\mu_m}-1},\]

where the choice set is partitioned into \(J_m\) nests, each associated with a parameter \(\mu_m\), and \(\mu\) is the scale parameter. The condition is \(0 \leq \mu \leq \mu_m\) must be verified. In general, \(\mu\) is normalized to 1.0.

This is an example with 5 alternatives. Nest A contains alternatives 1, 2 and 4, and is associated with a scale parameter \(\mu_A=1.2\). Nest B contains alternatives 3 and 5, and is associated with a scale parameter \(\mu_B=2.3\).

v = {1: Variable('Variable1'), 2: 0.1, 3: -0.1, 4: -0.2, 5: 0.2}
av = {1: 1, 2: 0, 3: 1, 4: 1, 5: 1}

Definition of the nests.

nest_a = OneNestForNestedLogit(
    nest_param=1.2, list_of_alternatives=[1, 2, 4], name='nest_a'
)
nest_b = OneNestForNestedLogit(
    nest_param=2.3, list_of_alternatives=[3, 5], name='name_b'
)

nests = NestsForNestedLogit(choice_set=list(v), tuple_of_nests=(nest_a, nest_b))

p1 = nested(v, availability=av, nests=nests, choice=1)
p1_value = evaluate_simple_expression_per_row(
    expression=p1,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Nested logit probability of alternative 1: {p1_value}')

Nested logit probability of alternative 1: [0.55789028 0.78684631 0.9138115  0.96786857 0.98836318]

If all the alternatives are available, define the availability dictionary as None.

p1_value = evaluate_simple_expression_per_row(
    expression=p1,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(
    f'Nested logit probability of alternative 1, all alternatives are available: {p1_value}'
)

Nested logit probability of alternative 1, all alternatives are available: [0.55789028 0.78684631 0.9138115  0.96786857 0.98836318]

The syntax is similar to obtain the log of the probability.

p2 = lognested(v, availability=av, nests=nests, choice=1)
p2_value = evaluate_simple_expression_per_row(
    expression=p2,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Nested logit log probability of alternative 1: {p2_value}')

Nested logit log probability of alternative 1: [-0.58359296 -0.23972233 -0.09013096 -0.03265898 -0.01170506]

p2 = lognested(v, availability=None, nests=nests, choice=1)
p2_value = evaluate_simple_expression_per_row(
    expression=p2,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(
    f'Nested logit log probability of alternative 1, all alternatives are available: {p2_value}'
)

Nested logit log probability of alternative 1, all alternatives are available: [-0.7677835  -0.31935224 -0.11821542 -0.04163899 -0.01446801]

If the value of the parameter \(\mu\) is not 1, there is another function to call. Note that, for the sake of computational efficiency, it is not verified by the code if the condition \(0 \leq \mu \leq \mu_m\) is valid.

p1 = nested_mev_mu(v, availability=av, nests=nests, choice=1, mu=1.1)
p1_value = evaluate_simple_expression_per_row(
    expression=p1,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Nested logit probability of alternative 1, mu=1.1: {p1_value}')

Nested logit probability of alternative 1, mu=1.1: [0.57151598 0.80643395 0.92814743 0.9755475  0.9919295 ]

p1 = lognested_mev_mu(v, availability=av, nests=nests, choice=1, mu=1.1)
p1_value = evaluate_simple_expression_per_row(
    expression=p1,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Nested logit log probability of alternative 1, mu=1.1: {p1_value}')

Nested logit log probability of alternative 1, mu=1.1: [-0.55946283 -0.21513329 -0.07456469 -0.02475643 -0.00810324]

The validity of the nested structure can be verified.

nest_c = OneNestForNestedLogit(nest_param=2.3, list_of_alternatives=[3], name='name_c')
nests = NestsForNestedLogit(choice_set=list(v), tuple_of_nests=(nest_a, nest_b))

is_valid, msg = nests.check_partition()

display(is_valid)

True

print(msg)

;

If an alternative belongs to two nests

nest_a = OneNestForNestedLogit(nest_param=1.2, list_of_alternatives=[1, 2, 3, 4])
nest_b = OneNestForNestedLogit(nest_param=2.3, list_of_alternatives=[3, 5])
nests = NestsForNestedLogit(choice_set=list(v), tuple_of_nests=(nest_a, nest_b))
is_valid, msg = nests.check_partition()

display(is_valid)

False

print(msg)

; The following alternatives appear both in nests nest_1 and nest_2: {3}.

Cross-nested logit model: the \(G\) function for the cross nested logit model is defined such that

\[G_i=\frac{\partial G}{\partial y_i}(e^{V_1},\ldots,e^{V_J}) = \mu \sum_{m=1}^{M} \alpha_{im}^{\frac{\mu_m}{\mu}} e^{(\mu_m-1) V_i}\left( \sum_{j=1}^{J} \alpha_{jm}^{\frac{\mu_m}{\mu}} e^{\mu_m V_j} \right)^{\frac{\mu}{\mu_m}-1},\]

where each nest \(m\) is associated with a parameter \(\mu_m\) and, for each alternative \(i\), a parameter \(\alpha_{im} \geq 0\) that captures the degree of membership of alternative \(i\) to nest \(m\). \(\mu\) is the scale parameter. For each alternative \(i\), there must be at least one nest \(m\) such that \(\alpha_{im}>0\). The condition \(0 \leq \mu \leq \mu_m\) must be also verified. In general, \(\mu\) is normalized to 1.0.

This is an example with 5 alternatives and two nests.

  • Alt. 1 belongs to nest A.

  • Alt. 2 belongs to nest A.

  • Alt. 3 belongs to both nest A (50%) and nest B (50%).

  • Alt. 4 belongs to nest B.

  • Alt. 5 belongs to nest B.

v = {1: Variable('Variable1'), 2: 0.1, 3: -0.1, 4: -0.2, 5: 0.2}
av = {1: 1, 2: 0, 3: 1, 4: 1, 5: 1}
alpha_a = {1: 1, 2: 1, 3: 0.5, 4: 0, 5: 0}
alpha_b = {1: 0, 2: 0, 3: 0.5, 4: 1, 5: 1}
nest_a = OneNestForCrossNestedLogit(
    nest_param=1.2, dict_of_alpha=alpha_a, name='Nest a'
)
nest_b = OneNestForCrossNestedLogit(
    nest_param=2.3, dict_of_alpha=alpha_b, name='Nest b'
)
nests = NestsForCrossNestedLogit(choice_set=list(v), tuple_of_nests=(nest_a, nest_b))

p1 = cnl(v, availability=av, nests=nests, choice=1)
p1_value = evaluate_simple_expression_per_row(
    expression=p1,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Cross-Nested logit probability of alternative 1: {p1_value}')

Cross-Nested logit probability of alternative 1: [0.60161076 0.81080413 0.92317655 0.97098919 0.98933903]

If all the alternatives are available, define the availability dictionary as None.

p1 = cnl(v, availability=None, nests=nests, choice=1)
p1_value = evaluate_simple_expression_per_row(
    expression=p1,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(
    f'Cross-Nested logit probability of alternative 1, all alternatives are available: {p1_value}'
)

Cross-Nested logit probability of alternative 1, all alternatives are available: [0.49345928 0.74695583 0.89735316 0.9622809  0.98660661]

If the value of the parameter \(\mu\) is not 1, there is another function to call. Note that, for the sake of computational efficiency, it is not verified by the code if the condition \(0 \leq \mu \leq \mu_m\) is verified.

p1 = cnlmu(v, availability=av, nests=nests, choice=1, mu=1.1)
p1_value = evaluate_simple_expression_per_row(
    expression=p1,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'Cross-Nested logit probability of alternative 1, mu = 1.1: {p1_value}')

Cross-Nested logit probability of alternative 1, mu = 1.1: [0.6110354  0.828654   0.93675704 0.97837752 0.99280536]

If the sample is endogenous, a correction must be included in the model, as proposed by Bierlaire, Bolduc and McFadden (2008). In this case, the generating function must first be defined, and the MEV model with correction is then called.

log_gi = get_mev_for_cross_nested(v, availability=av, nests=nests)
display(log_gi)

{1: logzero(MultipleSum([((PowerConstant(<Numeric value=1.0>, 1.2) * exp((<Numeric value=0.19999999999999996> * <Variable name=Variable1>))) * PowerConstant(MultipleSum([((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 1.2)) * exp((<Numeric value=1.2> * <Variable name=Variable1>))), ((<Numeric value=0.0> * PowerConstant(<Numeric value=1.0>, 1.2)) * exp(<Numeric value=0.12>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.5>, 1.2)) * exp(<Numeric value=-0.12>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 1.2)) * exp(<Numeric value=-0.24>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 1.2)) * exp(<Numeric value=0.24>))]), -0.16666666666666663)), ((PowerConstant(<Numeric value=0.0>, 2.3) * exp((<Numeric value=1.2999999999999998> * <Variable name=Variable1>))) * PowerConstant(MultipleSum([((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 2.3)) * exp((<Numeric value=2.3> * <Variable name=Variable1>))), ((<Numeric value=0.0> * PowerConstant(<Numeric value=0.0>, 2.3)) * exp(<Numeric value=0.22999999999999998>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.5>, 2.3)) * exp(<Numeric value=-0.22999999999999998>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 2.3)) * exp(<Numeric value=-0.45999999999999996>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 2.3)) * exp(<Numeric value=0.45999999999999996>))]), -0.5652173913043478))])), 2: logzero(MultipleSum([((PowerConstant(<Numeric value=1.0>, 1.2) * exp(<Numeric value=0.019999999999999997>)) * PowerConstant(MultipleSum([((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 1.2)) * exp((<Numeric value=1.2> * <Variable name=Variable1>))), ((<Numeric value=0.0> * PowerConstant(<Numeric value=1.0>, 1.2)) * exp(<Numeric value=0.12>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.5>, 1.2)) * exp(<Numeric value=-0.12>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 1.2)) * exp(<Numeric value=-0.24>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 1.2)) * exp(<Numeric value=0.24>))]), -0.16666666666666663)), ((PowerConstant(<Numeric value=0.0>, 2.3) * exp(<Numeric value=0.12999999999999998>)) * PowerConstant(MultipleSum([((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 2.3)) * exp((<Numeric value=2.3> * <Variable name=Variable1>))), ((<Numeric value=0.0> * PowerConstant(<Numeric value=0.0>, 2.3)) * exp(<Numeric value=0.22999999999999998>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.5>, 2.3)) * exp(<Numeric value=-0.22999999999999998>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 2.3)) * exp(<Numeric value=-0.45999999999999996>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 2.3)) * exp(<Numeric value=0.45999999999999996>))]), -0.5652173913043478))])), 3: logzero(MultipleSum([((PowerConstant(<Numeric value=0.5>, 1.2) * exp(<Numeric value=-0.019999999999999997>)) * PowerConstant(MultipleSum([((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 1.2)) * exp((<Numeric value=1.2> * <Variable name=Variable1>))), ((<Numeric value=0.0> * PowerConstant(<Numeric value=1.0>, 1.2)) * exp(<Numeric value=0.12>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.5>, 1.2)) * exp(<Numeric value=-0.12>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 1.2)) * exp(<Numeric value=-0.24>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 1.2)) * exp(<Numeric value=0.24>))]), -0.16666666666666663)), ((PowerConstant(<Numeric value=0.5>, 2.3) * exp(<Numeric value=-0.12999999999999998>)) * PowerConstant(MultipleSum([((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 2.3)) * exp((<Numeric value=2.3> * <Variable name=Variable1>))), ((<Numeric value=0.0> * PowerConstant(<Numeric value=0.0>, 2.3)) * exp(<Numeric value=0.22999999999999998>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.5>, 2.3)) * exp(<Numeric value=-0.22999999999999998>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 2.3)) * exp(<Numeric value=-0.45999999999999996>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 2.3)) * exp(<Numeric value=0.45999999999999996>))]), -0.5652173913043478))])), 4: logzero(MultipleSum([((PowerConstant(<Numeric value=0.0>, 1.2) * exp(<Numeric value=-0.039999999999999994>)) * PowerConstant(MultipleSum([((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 1.2)) * exp((<Numeric value=1.2> * <Variable name=Variable1>))), ((<Numeric value=0.0> * PowerConstant(<Numeric value=1.0>, 1.2)) * exp(<Numeric value=0.12>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.5>, 1.2)) * exp(<Numeric value=-0.12>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 1.2)) * exp(<Numeric value=-0.24>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 1.2)) * exp(<Numeric value=0.24>))]), -0.16666666666666663)), ((PowerConstant(<Numeric value=1.0>, 2.3) * exp(<Numeric value=-0.25999999999999995>)) * PowerConstant(MultipleSum([((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 2.3)) * exp((<Numeric value=2.3> * <Variable name=Variable1>))), ((<Numeric value=0.0> * PowerConstant(<Numeric value=0.0>, 2.3)) * exp(<Numeric value=0.22999999999999998>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.5>, 2.3)) * exp(<Numeric value=-0.22999999999999998>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 2.3)) * exp(<Numeric value=-0.45999999999999996>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 2.3)) * exp(<Numeric value=0.45999999999999996>))]), -0.5652173913043478))])), 5: logzero(MultipleSum([((PowerConstant(<Numeric value=0.0>, 1.2) * exp(<Numeric value=0.039999999999999994>)) * PowerConstant(MultipleSum([((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 1.2)) * exp((<Numeric value=1.2> * <Variable name=Variable1>))), ((<Numeric value=0.0> * PowerConstant(<Numeric value=1.0>, 1.2)) * exp(<Numeric value=0.12>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.5>, 1.2)) * exp(<Numeric value=-0.12>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 1.2)) * exp(<Numeric value=-0.24>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 1.2)) * exp(<Numeric value=0.24>))]), -0.16666666666666663)), ((PowerConstant(<Numeric value=1.0>, 2.3) * exp(<Numeric value=0.25999999999999995>)) * PowerConstant(MultipleSum([((<Numeric value=1.0> * PowerConstant(<Numeric value=0.0>, 2.3)) * exp((<Numeric value=2.3> * <Variable name=Variable1>))), ((<Numeric value=0.0> * PowerConstant(<Numeric value=0.0>, 2.3)) * exp(<Numeric value=0.22999999999999998>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=0.5>, 2.3)) * exp(<Numeric value=-0.22999999999999998>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 2.3)) * exp(<Numeric value=-0.45999999999999996>)), ((<Numeric value=1.0> * PowerConstant(<Numeric value=1.0>, 2.3)) * exp(<Numeric value=0.45999999999999996>))]), -0.5652173913043478))]))}

Assume the following correction factors

correction = {1: -0.1, 2: 0.1, 3: 0.2, 4: -0.2, 5: 0}
p1 = mev_endogenous_sampling(v, log_gi, av, correction, choice=1)
p1_value = evaluate_simple_expression_per_row(
    expression=p1,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'MEV model probability with correction: {p1_value}')

MEV model probability with correction: [0.57460723 0.79415806 0.91584339 0.96822294 0.98835331]

correction = {1: -0.1, 2: 0.1, 3: 0.2, 4: -0.2, 5: 0}
p1 = logmev_endogenous_sampling(v, log_gi, av, correction, choice=1)
p1_value = evaluate_simple_expression_per_row(
    expression=p1,
    database=my_data,
    numerically_safe=False,
    second_derivatives_mode=SecondDerivativesMode.NEVER,
    use_jit=True,
)
display(f'MEV model log probability with correction: {p1_value}')

MEV model log probability with correction: [-0.55406855 -0.23047277 -0.0879099  -0.03229291 -0.01171504]

The MEV generating function for the following models are available.

Nested logit model

v = {1: Variable('Variable1'), 2: 0.1, 3: -0.1, 4: -0.2, 5: 0.2}
nest_a = OneNestForNestedLogit(
    nest_param=Beta('muA', 1.2, 1.0, None, 0), list_of_alternatives=[1, 2, 4]
)
nest_b = OneNestForNestedLogit(
    nest_param=Beta('muB', 2.3, 1.0, None, 0), list_of_alternatives=[3, 5]
)
nests = NestsForNestedLogit(choice_set=list(v), tuple_of_nests=(nest_a, nest_b))

log_gi = get_mev_for_nested(v, availability=None, nests=nests)
display(log_gi)

{1: (((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Variable name=Variable1>) + (((<Numeric value=1.0> / <Beta name=muA value=1.2 status=0>) - <Numeric value=1.0>) * log(MultipleSum([exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))])))), 2: (((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=0.1>) + (((<Numeric value=1.0> / <Beta name=muA value=1.2 status=0>) - <Numeric value=1.0>) * log(MultipleSum([exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))])))), 4: (((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=-0.2>) + (((<Numeric value=1.0> / <Beta name=muA value=1.2 status=0>) - <Numeric value=1.0>) * log(MultipleSum([exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))])))), 3: (((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=-0.1>) + (((<Numeric value=1.0> / <Beta name=muB value=2.3 status=0>) - <Numeric value=1.0>) * log(MultipleSum([exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>)), exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>))])))), 5: (((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=0.2>) + (((<Numeric value=1.0> / <Beta name=muB value=2.3 status=0>) - <Numeric value=1.0>) * log(MultipleSum([exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>)), exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>))]))))}

And with the \(\mu\) parameter.

log_gi = get_mev_for_nested_mu(v, availability=None, nests=nests, mu=1.1)
display(log_gi)

{1: ((log(<Numeric value=1.1>) + ((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Variable name=Variable1>)) + (((<Numeric value=1.1> / <Beta name=muA value=1.2 status=0>) - <Numeric value=1.0>) * log(MultipleSum([exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))])))), 2: ((log(<Numeric value=1.1>) + ((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=0.1>)) + (((<Numeric value=1.1> / <Beta name=muA value=1.2 status=0>) - <Numeric value=1.0>) * log(MultipleSum([exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))])))), 4: ((log(<Numeric value=1.1>) + ((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=-0.2>)) + (((<Numeric value=1.1> / <Beta name=muA value=1.2 status=0>) - <Numeric value=1.0>) * log(MultipleSum([exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>)), exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))])))), 3: ((log(<Numeric value=1.1>) + ((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=-0.1>)) + (((<Numeric value=1.1> / <Beta name=muB value=2.3 status=0>) - <Numeric value=1.0>) * log(MultipleSum([exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>)), exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>))])))), 5: ((log(<Numeric value=1.1>) + ((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=0.2>)) + (((<Numeric value=1.1> / <Beta name=muB value=2.3 status=0>) - <Numeric value=1.0>) * log(MultipleSum([exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>)), exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>))]))))}

Cross nested logit model

v = {1: Variable('Variable1'), 2: 0.1, 3: -0.1, 4: -0.2, 5: 0.2}
av = {1: 1, 2: 0, 3: 1, 4: 1, 5: 1}
alpha_a = {1: 1, 2: 1, 3: 0.5, 4: 0, 5: 0}
alpha_b = {1: 0, 2: 0, 3: 0.5, 4: 1, 5: 1}
nest_a = OneNestForCrossNestedLogit(
    nest_param=Beta('muA', 1.2, 1.0, None, 0), dict_of_alpha=alpha_a
)
nest_b = OneNestForCrossNestedLogit(
    nest_param=Beta('muB', 2.3, 1.0, None, 0), dict_of_alpha=alpha_b
)
nests = NestsForCrossNestedLogit(choice_set=list(v), tuple_of_nests=(nest_a, nest_b))

log_gi = get_mev_for_cross_nested(v, availability=None, nests=nests)
display(log_gi)

{1: logzero(MultipleSum([(((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp(((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Variable name=Variable1>))) * (MultipleSum([((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>))), ((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.1>))), ((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))), ((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.0> - <Beta name=muA value=1.2 status=0>) / <Beta name=muA value=1.2 status=0>))), (((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp(((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Variable name=Variable1>))) * (MultipleSum([((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Variable name=Variable1>))), ((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>))), ((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.2>))), ((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.0> - <Beta name=muB value=2.3 status=0>) / <Beta name=muB value=2.3 status=0>)))])), 2: logzero(MultipleSum([(((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp(((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=0.1>))) * (MultipleSum([((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>))), ((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.1>))), ((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))), ((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.0> - <Beta name=muA value=1.2 status=0>) / <Beta name=muA value=1.2 status=0>))), (((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp(((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=0.1>))) * (MultipleSum([((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Variable name=Variable1>))), ((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>))), ((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.2>))), ((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.0> - <Beta name=muB value=2.3 status=0>) / <Beta name=muB value=2.3 status=0>)))])), 3: logzero(MultipleSum([(((<Numeric value=0.5> ** <Beta name=muA value=1.2 status=0>) * exp(((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=-0.1>))) * (MultipleSum([((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>))), ((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.1>))), ((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))), ((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.0> - <Beta name=muA value=1.2 status=0>) / <Beta name=muA value=1.2 status=0>))), (((<Numeric value=0.5> ** <Beta name=muB value=2.3 status=0>) * exp(((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=-0.1>))) * (MultipleSum([((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Variable name=Variable1>))), ((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>))), ((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.2>))), ((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.0> - <Beta name=muB value=2.3 status=0>) / <Beta name=muB value=2.3 status=0>)))])), 4: logzero(MultipleSum([(((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp(((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=-0.2>))) * (MultipleSum([((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>))), ((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.1>))), ((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))), ((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.0> - <Beta name=muA value=1.2 status=0>) / <Beta name=muA value=1.2 status=0>))), (((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp(((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=-0.2>))) * (MultipleSum([((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Variable name=Variable1>))), ((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>))), ((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.2>))), ((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.0> - <Beta name=muB value=2.3 status=0>) / <Beta name=muB value=2.3 status=0>)))])), 5: logzero(MultipleSum([(((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp(((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=0.2>))) * (MultipleSum([((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>))), ((<Numeric value=1.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.1>))), ((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))), ((<Numeric value=0.0> ** <Beta name=muA value=1.2 status=0>) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.0> - <Beta name=muA value=1.2 status=0>) / <Beta name=muA value=1.2 status=0>))), (((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp(((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=0.2>))) * (MultipleSum([((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Variable name=Variable1>))), ((<Numeric value=0.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>))), ((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.2>))), ((<Numeric value=1.0> ** <Beta name=muB value=2.3 status=0>) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.0> - <Beta name=muB value=2.3 status=0>) / <Beta name=muB value=2.3 status=0>)))]))}

Cross nested logit model with \(\mu\) parameter.

log_gi = get_mev_for_cross_nested_mu(v, availability=None, nests=nests, mu=1.1)
display(log_gi)

{1: log((<Numeric value=1.1> * MultipleSum([(((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp(((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Variable name=Variable1>))) * (MultipleSum([((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>))), ((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.1>))), ((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))), ((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.1> / <Beta name=muA value=1.2 status=0>) - <Numeric value=1.0>))), (((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp(((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Variable name=Variable1>))) * (MultipleSum([((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Variable name=Variable1>))), ((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>))), ((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.2>))), ((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.1> / <Beta name=muB value=2.3 status=0>) - <Numeric value=1.0>)))]))), 2: log((<Numeric value=1.1> * MultipleSum([(((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp(((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=0.1>))) * (MultipleSum([((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>))), ((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.1>))), ((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))), ((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.1> / <Beta name=muA value=1.2 status=0>) - <Numeric value=1.0>))), (((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp(((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=0.1>))) * (MultipleSum([((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Variable name=Variable1>))), ((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>))), ((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.2>))), ((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.1> / <Beta name=muB value=2.3 status=0>) - <Numeric value=1.0>)))]))), 3: log((<Numeric value=1.1> * MultipleSum([(((<Numeric value=0.5> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp(((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=-0.1>))) * (MultipleSum([((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>))), ((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.1>))), ((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))), ((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.1> / <Beta name=muA value=1.2 status=0>) - <Numeric value=1.0>))), (((<Numeric value=0.5> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp(((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=-0.1>))) * (MultipleSum([((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Variable name=Variable1>))), ((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>))), ((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.2>))), ((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.1> / <Beta name=muB value=2.3 status=0>) - <Numeric value=1.0>)))]))), 4: log((<Numeric value=1.1> * MultipleSum([(((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp(((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=-0.2>))) * (MultipleSum([((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>))), ((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.1>))), ((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))), ((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.1> / <Beta name=muA value=1.2 status=0>) - <Numeric value=1.0>))), (((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp(((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=-0.2>))) * (MultipleSum([((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Variable name=Variable1>))), ((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>))), ((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.2>))), ((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.1> / <Beta name=muB value=2.3 status=0>) - <Numeric value=1.0>)))]))), 5: log((<Numeric value=1.1> * MultipleSum([(((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp(((<Beta name=muA value=1.2 status=0> - <Numeric value=1.0>) * <Numeric value=0.2>))) * (MultipleSum([((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Variable name=Variable1>))), ((<Numeric value=1.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.1>))), ((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=-0.2>))), ((<Numeric value=0.0> ** (<Beta name=muA value=1.2 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muA value=1.2 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.1> / <Beta name=muA value=1.2 status=0>) - <Numeric value=1.0>))), (((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp(((<Beta name=muB value=2.3 status=0> - <Numeric value=1.0>) * <Numeric value=0.2>))) * (MultipleSum([((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Variable name=Variable1>))), ((<Numeric value=0.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.1>))), ((<Numeric value=0.5> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.1>))), ((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=-0.2>))), ((<Numeric value=1.0> ** (<Beta name=muB value=2.3 status=0> / <Numeric value=1.1>)) * exp((<Beta name=muB value=2.3 status=0> * <Numeric value=0.2>)))]) ** ((<Numeric value=1.1> / <Beta name=muB value=2.3 status=0>) - <Numeric value=1.0>)))])))}

Total running time of the script: (0 minutes 2.203 seconds)

Gallery generated by Sphinx-Gallery